3D Statics Problem

The following three-dimensional statics problem is taken from the book Engineering Mechanics: Statics, 8th edition, by J. L. Meriam, et al. The solution algorithm was created using the Jupyter Notebook and the Python programming language.

Problem 3/076

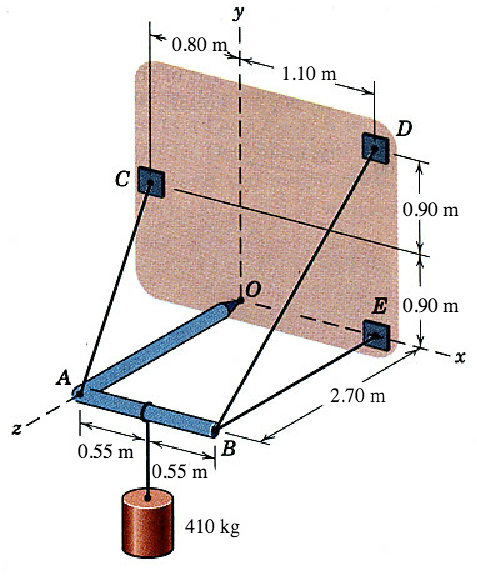
The light right-angle boom which supports the 410-kg cylinder is supported by three cables and a ball-and-socket joint at O attached to the vertical x-y surface. Determine the reactions at O and the cable tensions.

import numpy as np

# Mass on a string (kg)
m = 410

# Acceleration of gravity (m/s^2)
g = 9.81

# Position vectors of each point
# (Point G is where the mass string is tied to the boom)
A = np.array([ 0.00, 0.0, 2.7])
B = np.array([ 1.10, 0.0, 2.7])
C = np.array([-0.80, 0.9, 0.0])
D = np.array([ 1.10, 1.8, 0.0])
E = np.array([ 1.10, 0.0, 0.0])
G = np.array([ 0.55, 0.0, 2.7])

# Weight force vector
W = np.array([0, -m*g, 0])

# Radius vectors
OA = A
OG = G
OB = B

# Tension vectors
AC = C - A
BD = D - B
BE = E - B

# Tension unit vectors
uAC = AC / np.linalg.norm(AC)
uBD = BD / np.linalg.norm(BD)
uBE = BE / np.linalg.norm(BE)

# Create a 3x3 matrix
M = np.zeros(shape=(3,3))

# Populate cols of matrix with moment vectors
M[:,0] = np.cross(OA, uAC)
M[:,1] = np.cross(OB, uBD)
M[:,2] = np.cross(OB, uBE)

print(M)

[[-0.822 -1.498 -0.   ]
 [-0.731  0.915  1.1  ]
 [ 0.     0.61   0.   ]]

# The three tension moments must cancel the weight moment
w = -np.cross(OG, W)

print(w)

[-10859.67      -0.      2212.155]

# Solve the matrix for the tension magnitudes
T = np.linalg.solve(M,w)

T_AC = T[0]
T_BD = T[1]
T_BE = T[2]

# Reaction forces at O
Ox = -T_AC * uAC[0]
Oy = -T_AC * uAC[1] - T_BD * uBD[1] - W[1]
Oz = -T_AC * uAC[2] - T_BD * uBD[2] - T_BE * uBE[2]

# Final results
print("T_AC = {:06.1f} N\nT_BD = {:06.1f} N\nT_BE = {:06.1f} N\n"
      .format(T_AC,T_BD,T_BE))
print("Ox = {:06.1f} N \nOy = {:01.1f} N \nOz = {:06.1f} N"
      .format(Ox,Oy,Oz))

T_AC =  6606.0 N
T_BD =  3625.5 N
T_BE =  1371.2 N

Ox   =  1787.6 N
Oy   =     0.0 N
Oz   = 10420.9 N